De l’utilisation des dés
A l’exception de quelques titres qui tiennent généralement de l’expérimentation ludique, la totalité de nos jeux de rôle et de nos jeux de stratégie utilisent des dés d’une façon ou d’une autre. Intéressons-nous donc justement un instant aux différentes façons dont on peut utiliser des dés.
Rouler haut ou rouler bas
Dans certains jeux les joueurs sont appelés à rouler le plus haut possible (c’est à dire qu’ils espèrent obtenir les valeurs les plus élevées possibles sur les dés). Dans d’autres, on cherche à rouler le plus bas possible.
Ceci est dû au fait que de nombreuses règles de simulation sont basées sur l’exploitation d’un seuil. Dans le cas des jeux dans lesquels on roule haut, il s’agit d’un seuil au delà duquel on enregistre une réussite. Dans le cas des jeux dans lesquels on roule bas, il s’agit d’un seuil en deçà duquel la réussite est validée.
A priori il peut paraître plus intuitif de demander au joueur de rouler haut car on est habitué, pas toujours à raison, à penser que le plus est le mieux.
Seulement, certains jeux utilisent directement les capacités du personnages ou de l’entité que contrôle le joueur pour calculer le seuil de réussite. Dans ce cas la notion de « le plus est le mieux » s’applique prioritairement à la valeur de cette capacité plutôt qu’au jet de dés. On cherche alors naturellement à rouler en dessous de ladite capacité.
C’est notamment le cas dans les jeux qui expriment ces capacités sous forme de pourcentages de chances de réussite. Il paraît alors naturel de jeter 1D100 sous ce pourcentage.
Quoi qu’il en soit il est toujours possible de convertir un système qui incite à rouler bas en un système qui incite à rouler et et vice versa avec une stricte équivalence des probabilités. Pour cela, il suffit de calculer le complément du seuil de réussite sur le nombre de face du dé utilisé plus une (dans la mesure ou on comprend la borne dans les valeurs de réussite).
Pour reprendre l’exemple du pourcentage sous lequel on cherche à rouler bas, il suffit de prendre la différence entre 101 et la valeur du pourcentage et de rouler haut au dessus de ce seuil. Par exemple, pour un jet sous 30 %, on obtient les mêmes probabilités que pour un jet au dessus de 71 (101 - 30). En d’autres termes, on a exactement les même chance d’obtenir 71 ou plus que 30 ou moins sur 1D100, soit 30 chances sur 100.
Effet du nombre de dés jetés
Comme il existe une grande variété de dés en ce qui concerne le nombre de faces qu’ils présentent (D4, D6, D10, D12, D20, D30, D100…), beaucoup de systèmes se contentent de requérir le jet d’un seul dé pour régler la plupart des situations.
Répartition des probabilités sur 1D6
| Valeur | Probabilité |
|---|---|
| 1 | 1 / 6 soit 16,67 % |
| 1 | 2 / 6 soit 16,67 % |
| 1 | 3 / 6 soit 16,67 % |
| 1 | 4 / 6 soit 16,67 % |
| 1 | 5 / 6 soit 16,67 % |
| 1 | 6 / 6 soit 16,67 % |
Le fait de jeter un unique dé entraîne une répartition uniforme des probabilités de sortie de chacune des faces. Pour 1D6, chaque face a exactement 1 chance sur 6 de sortir (sauf si le dé est pipé, bien sûr). Pour 1D20, chaque face a exactement 1 chance sur 20 de sortir. Comme chaque face présente généralement une valeur différente (à moins encore qu’il ne s’agisse de dés spéciaux ou truqués), on obtient une équiprobabilité des différentes valeurs possibles.
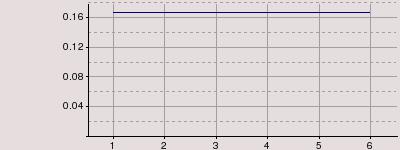
Quand on exprime la probabilité en fonction de la valeur obtenue à l’issue du jet de dés, cette équiprobabilité se représente graphiquement par une droite horizontale qui traverse la plage des valeurs possible.
Ce n’est plus le cas dès lors que l’on jette au moins deux dés.
Répartition des probabilités sur 2D6
| Valeur | Probabilité |
|---|---|
| 2 | 1 / 36 soit 2,78 % |
| 3 | 2 / 36 soit 5,56 % |
| 4 | 3 / 36 soit 8,33 % |
| 5 | 4 / 36 soit 11,11 % |
| 6 | 5 / 36 soit 13,89 % |
| 7 | 6 / 36 soit 16,67 % |
| 8 | 5 / 36 soit 13,89 % |
| 9 | 4 / 36 soit 11,11 % |
| 10 | 3 / 36 soit 8,33 % |
| 11 | 2 / 36 soit 5,56 % |
| 12 | 1 / 36 soit 2,78 % |
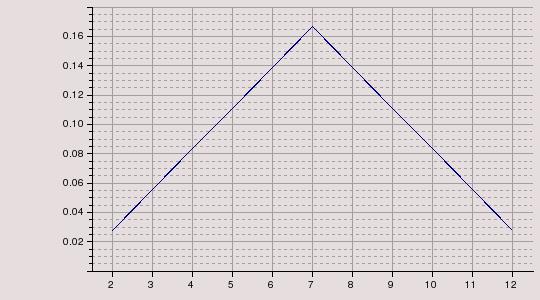
Par exemple, lorsque l’on jette 2D6, on peut obtenir toutes les valeurs entières comprises entre 2 et 12, soit seulement 11 valeurs différentes alors qu’il existe 36 possibilités (les 6 du premier dé multipliées par les 6 du second dé). Parmi ces 36 possibilités il n’y en a qu’une seule qui aboutie sur la valeur 2 : le fait d’obtenir à la fois 1 sur le premier dé et 1 sur le second dé. Mais deux possibilités différentes permettent d’obtenir la valeur 3 : la première est celle où l’obtient 1 sur le premier dé et 2 sur le second, la deuxième est celle où l’on obtient 2 sur le premier dé et 1 sur le second.
On a donc deux fois plus de chances d’obtenir un 3 qu’un 2 (2 chances sur 36 pour le 3 contre 1 chance sur 36 pour le 2). L’équiprobabilité des valeurs est bel et bien rompue.
En fait, quand on lance plusieurs dés, les valeurs proches de la moyenne de la plage des valeurs possibles sont plus probables que les valeurs proches des borne de cette plage. On observe même une symétrie autour de la moyenne.
Par exemple, dans le cas de 2D6, la valeur 12 a comme la valeur 2 une seule chance sur 36 de sortir : il faut obtenir 6 sur le premier dé et 6 sur le second. Les deux bornes ont donc la même probabilité.
On peut donc parler de répartition de probabilités centrée sur la moyenne des valeurs possibles. Dans le cas où on jette deux dés, le graphique de répartition des probabilités en fonction des valeur prendra la forme d’une pyramide dont la pointe se trouve précisément sur la valeur moyenne.
Quand on lance 3 dés ou plus, le graphique prend une valeur de courbe en cloche. Et plus le nombre de dés lancés sera grand plus la cloche sera étirée en hauteur sur la moyenne.
Répartition des probabilités sur 3D6
| Valeur | Probabilité |
|---|---|
| 3 | 1 / 216 soit 0,46 % |
| 4 | 3 / 216 soit 1,38 % |
| 5 | 6 / 216 soit 2,77 % |
| 6 | 10 / 216 soit 4,62 % |
| 7 | 15 / 216 soit 6,94 % |
| 8 | 21 / 216 soit 9,72 % |
| 9 | 25 / 216 soit 11,57 % |
| 10 | 27 / 216 soit 12,5 % |
| 11 | 27 / 216 soit 12,5 % |
| 12 | 25 / 216 soit 11,57 % |
| 13 | 21 / 216 soit 9,72 % |
| 14 | 15 / 216 soit 6,94 % |
| 15 | 10 / 216 soit 4,62 % |
| 16 | 6 / 216 soit 2,77 % |
| 17 | 3 / 216 soit 1,38 % |
| 18 | 1 / 216 soit 0,46 % |
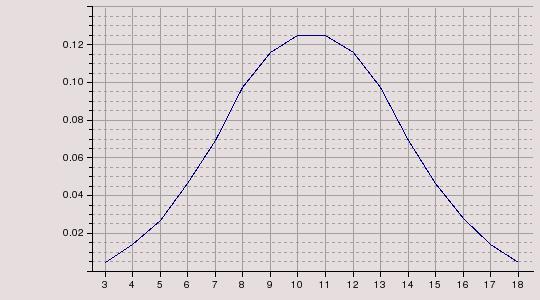
Ce recentrage des valeurs obtenues sur la moyenne est exploitée dans certains jeux qui cherchent à obtenir des situations plus réalistes1. Si les valeurs extrêmes doivent entraîner des conséquences qualifiées d’exceptionnelles dans le jeu (comme les notions de réussites ou d’échecs critiques présentes dans certains systèmes de jeu de rôle) alors il peut effectivement être souhaitable que ces valeurs soit moins probables que les autres. Sans cela, l’exceptionnel devient aussi courant que le normal et il perd son caractère exceptionnel.
Les dés de puissance
Dans ce qui précède, quand j’ai traité de jets de plusieurs dés je n’ai envisagé que l’hypothèse de faire la somme des résultats obtenus. Mais il existe au moins une autre façon de jeter plusieurs dés.
C’est celle que l’on utilise par exemple quand on lance deux D10 pour représenter 1D100. L’un des dés représente les dizaines et l’autre représente les unités (rappelons que les faces des D10 sont généralement numérotées de 0 à 9 et qu’un double 0 est considéré comme un 100).
Et l’on peut étendre le principe. Si l’on jette un troisième dé pour représenter les centaines, on obtient 1D1000.
En fait, chaque D10 représente une puissance de 10. On multiplie la valeur du dé des unités par 10⁰, soit 1. On multiplie la valeur du dé des dizaines par 10¹, soit 10. On multiplie la valeur du dé des centaines par 10², soit 100. Et ainsi de suite…
Cette approche est du même ordre d’astuce pour s’affranchir des limites matérielles des dés que celle du système des chiffres arabes pour éviter d’avoir à tracer mille petits bâtons pour écrire le nombre 1000. Et l’on obtient bien une équiprobabilité sur la plage des valeurs possibles exactement comme si l’on lançait un seul dé.
Le D10 est particulièrement approprié à cette approche du fait que d’une part son nombre de face correspond à nos habitudes de système décimal (encore les chiffres arabes) et que d’autre part ses faces sont numérotées de 0 à 9 plutôt que de 1 à 10. Mais le même principe pourrait être appliqué avec d’autres type de dés.
On pourrait par exemple obtenir 1D36 en base 6 en lançant deux D6 et en considérant le faces numérotées 6 comme des 0.
Dés multiples indépendants
D’autres systèmes de règles, comme ceux des jeux de rôle Shadowrun ou Vampires, la Masquarade, proposent encore une autre approche dans le domaine du jet de plusieurs dés.
On jette plusieurs dés mais l’on n’en effectue pas la somme. Chaque dés est comparé à un seuil. Chaque dé supérieur ou égal au seuil (dans le cas où l’on cherche à « rouler haut ») apporte un point de réussite.
Cette approche permet d’évaluer la qualité du jet selon plusieurs critères comme le nombre de réussites unitaires obtenues d’une part et la marge par rapport au seuil de réussite du dé le plus haut d’autre part. Personnellement je trouve cela un peu confus.
Cette approche découle généralement de ce que le jeu tente de modéliser les capacités des personnages par des nombres de dés à jeter. Notons au passage que si les dés de puissance constituent comme nous l’avons vu une utilisation particulièrement astucieuse pour améliorer le rapport entre le nombre de dés jetés et la plage des valeurs possibles, c’est exactement le contraire en ce qui concerne cette approche des dés multiples indépendants : on peut se retrouver à jeter un nombre invraisemblable de dés sans que cela n’augmente la plage des valeurs possibles.
N dés parmi M
Une autre approche consiste à jeter un certain nombre de dés et à n’en retenir qu’une partie dans le calcul du résultat du jet. Il peut par exemple s’agir de lancer 3D6 et de n’en retenir que les 2 plus élevés pour le résultat. Il pourrait tout aussi bien s’agir des 2 moins élevés si cela était utile dans les règles.
Cette approche a un intérêt ludique indéniable en ce qu’elle permet de modifier la répartition des probabilités en l’excentrant en direction de l’une des deux bornes plutôt que sur la moyenne, sans toutefois changer la plage des valeurs possibles sur les dés retenus.
Par exemple, quand on lance simplement 2D6, on peut obtenir des valeurs comprise entre 2 et 12 selon une répartition de probabilité centrée sur la valeur moyenne qui est 7.
Répartition des probabilités sur 2D6
| Valeur | Probabilité |
|---|---|
| 2 | 1 / 36 soit 2,78 % |
| 3 | 2 / 36 soit 5,56 % |
| 4 | 3 / 36 soit 8,33 % |
| 5 | 4 / 36 soit 11,11 % |
| 6 | 5 / 36 soit 13,89 % |
| 7 | 6 / 36 soit 16,67 % |
| 8 | 5 / 36 soit 13,89 % |
| 9 | 4 / 36 soit 11,11 % |
| 10 | 3 / 36 soit 8,33 % |
| 11 | 2 / 36 soit 5,56 % |
| 12 | 1 / 36 soit 2,78 % |

Si on jette 3D6 et que l’on conserve les deux plus élevés pour le résultat, la plage des valeurs disponible reste inchangée : entre 2 et 12. Par contre la répartition des probabilités n’est plus la même, on comprend aisément que l’on a plus de chance d’obtenir des résultats supérieurs à 7.
Répartition des probabilités sur 2D6 parmi 3 en conservant les plus élevés
| Valeur | Probabilité |
|---|---|
| 2 | 1 / 216 soit 0,46 % |
| 3 | 3 / 216 soit 1,39 % |
| 4 | 7 / 216 soit 3,24 % |
| 5 | 12 / 216 soit 5,56 % |
| 6 | 19 / 216 soit 8,8 % |
| 7 | 27 / 216 soit 12,5 % |
| 8 | 34 / 216 soit 15,74 % |
| 9 | 36 / 216 soit 16,67 % |
| 10 | 34 / 216 soit 15,74 % |
| 11 | 27 / 216 soit 12,5 % |
| 12 | 16 / 216 soit 7,41 % |
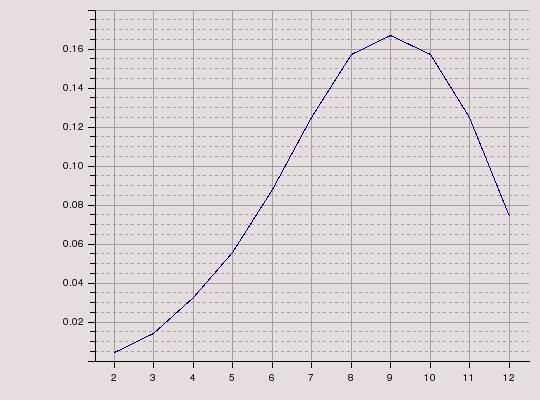
Comme nous pouvons le constater, la répartition des probabilités se trouve excentrée du 7 vers le 9 (en plus du fait de prendre une forme de cloche).
Nous détenons avec cette approche un outil précieux pour représenter des conditions influençant favorablement ou défavorablement un jet de dé sans toutefois modifier la plage des valeurs possibles comme le ferait un simple modificateur appliqué au résultat du jet (jetez 2D6+1 et vous obtenez une plage qui va de 3 à 13 et non plus de 2 à 12).
Pour illustrer ce que un dé unique peut induire d’irréalisme avec son équiprobabilité des valeurs, je ne résiste pas à l’envie de citer le cas des échec critiques dans les jeux à base de D20, comme Dungeons & Dragons. Dans ce jeux le scène de combat sont décomposées en rounds dont chacun représente 6 secondes pour le personnage. En général, un personnage peut effectuer une attaque à chaque round et le joueur lance 1D20 pour voir si son attaque réussie ou échoue.
De nombreux meneurs de jeu établissent que quand le joueur obtient une valeur de 1 sur le D20 (soit 1 fois sur 20 en moyenne), son personnage est victime d’une maladresse : par exemple son arme lui échappe des mains et tombe au sol. Cela lui arrivera donc en moyenne 1 round sur 20 soit toutes les deux minutes (20 × 6 secondes). Imagine t’on un guerrier correctement entraîné (et les personnages de Dungeons & Dragons sont généralement censés l’être) laisser tomber son épée au sol toutes les deux minutes pendant une bataille ?↩︎